«Uh, è vero, non si capisce cosa succede. Sembra che ci sia una certa regolarità, però».
«Sì, è vero. Possiamo parlare solo di probabilità di cadere all'interno di un determinato intervallo, ma non ci sono orbite regolari stabili».
«Stabili?».
«Sì. Provo a spiegarmi: se ci pensi un attimo, il punto di intersezione tra la retta e la parabola è un punto fisso. Se prendi il valore iniziale giusto, cadi proprio sopra a quel punto e da lì non ti muovi più».
«Ah, già. Se il primo segmento verticale arriva proprio sopra a quel punto, quando mi muovo in orizzontale non mi sposto, rimango sempre lì».
«Esatto. In effetti di punti di intersezione tra la retta e la parabola ce ne sono due. Anche il valore 0 è stabile».
«Giusto. Se non c'è popolazione, nessuno si riproduce e nessuno muore».
«Proprio così. Ma se ti sposti anche di pochissimo da quei due punti di equilibrio, può succedere di tutto. E man mano che r aumenta, si nota sempre meno regolarità. Eccoti il grafico per il valore massimo di r, cioè 4».
«Eh, mamma mia. Qui sembra proprio che non ci sia regolarità».
«Già. Questo è quello che si chiama caos deterministico».
«Cosa significa?».
«Deterministico significa che il sistema è governato da una equazione esatta, non da probabilità. Sappiamo fare i calcoli, conosciamo le formule (che, fra l'altro, sono anche molto semplici), sappiamo esattamente cosa succederà alla generazione n+1, una volta che conosciamo lo stato della generazione n».
«Però c'è caos».
«Esatto. Una caratteristica del caos è questa: l'evoluzione del sistema dipende in maniera molto sensibile dalle condizioni iniziali».
«Cioè da come si parte?».
«Sì. Ricordi quando non c'era caos? Potevi partire da qualsiasi condizione iniziale, e prima o poi saresti arrivato all'equilibrio, che poteva essere un punto solo, oppure quella che abbiamo chiamato orbita. Anche se il sistema oscilla tra più punti, l'insieme di quei punti si chiama stabile perché il sistema tende ad assumere quella configurazione».
«Mi ricordo. Adesso invece non è più così, vero?».
«No. Due condizioni iniziali anche molto vicine prima o poi se ne vanno per strade molto diverse. Ti faccio un esempio, nella figura qua sotto, in cui la parabola ha r = 4, ho assegnato ad un punto il valore di x = 0.2, a un secondo punto ho assegnato invece x = 0.201. Ecco la prima generazione:».
«Praticamente non si nota la differenza».
«No, infatti, non abbiamo abbastanza pixel per notarla. Ecco cosa succede dopo tre generazioni:».
«Forse si comincia a vedere qualcosa».
«Sì, se ingrandisci la figura vedi due colori diversi. Ma ti basta aspettare un altro paio di generazioni per distinguere bene le due traiettorie:».
«Sono ancora abbastanza vicine, però».
«Sì, ma non lo rimarranno per molto. Dopo 9 iterazioni sono già molto staccate:».
«Sì, ormai non hanno più molto in comune».
«E andando avanti è sempre peggio. Ti faccio vedere un'ultima immagine, con 50 generazioni:».
«Sì, è davvero un caos».
«E questa è stata una grossissima delusione per Laplace».
«Perché?».
«Perché lui pensava che le leggi fisiche della meccanica, leggi semplici che descrivono il moto dei corpi, una volta note le condizioni iniziali, potessero essere usate per prevedere tutto».
«Tutto?».
«Sì, lui diceva datemi le condizioni iniziali, e vi saprò prevedere l'evoluzione dell'intero universo».
«E gli è andata male».
«Già. Una semplice legge come questa, con una facile curva di secondo grado, è imprevedibile. Mi basta sbagliare di pochissimo una condizione iniziale, e non riesco più a sapere quello che succederà dopo molte iterazioni. E, dato che le misure fisiche hanno sempre un margine di errore, tanti saluti al determinismo».
«E alle previsioni del tempo».
«Anche».
«Mi piacerebbe fare qualche prova con il sistema della crescita con risorse limitate: come hai fatto a fare i grafici?».
«Ho usato GeoGebra e seguito queste istruzioni, per non dover fare tutto a mano. Se vuoi, qui c'è un'applet java già pronta per giocarci».
«Ottimo».
«Concludo con un'ultima immagine, fatta da un utente di wikipedia. Immagina di voler creare un grafico che riassuma il comportamento del nostro sistema, per ogni valore di r fino a 4. Questa volta non vuoi vedere tutte le iterazioni, ma solo gli attrattori, cioè solo quello che succede quando la situazione è stabile».
«Ma non è sempre stabile».
«Vero. Immagina di partire da un punto a caso, poi di fare molte iterazioni (nell'immagine ne sono state fatte 1000) a vuoto. Poi cominci a raccogliere i dati: per ogni valore di r ne raccogli 100000».
«Sono tanti, cosa me ne faccio?».
«Quando r è piccolo otterrai 100000 valori tutti uguali, perché avrai un solo punto fisso».
«Infatti».
«Bene, allora cominci a creare un grafico. Sull'asse delle ascisse metti il valore di r che stai usando, sull'asse delle ordinate metti i valori di quei 100000 punti».
«Per r piccolo però metto un punto solo, no?».
«Certo, all'inizio disegnerai una curva: man mano che r cresce vedrai il punto fisso che cambia un po' posizione».
«Poi però c'è il raddoppio del periodo».
«Sì, a un certo punto vedrai la curva che si biforca. E dopo un po' vedrai le due biforcazioni dividersi ancora…».
«Perché siamo arrivati al periodo 4, giusto?».
«Esatto. Poi le biforcazioni si fanno sempre più frequenti, e a un certo punto diventano infinite».
«E dopo comincia il caos».
«Sì, siamo intorno a r = 3.569945672».
«Dopo si anneriranno tutti i punti, no?».
«Sì, dopo avremmo un grafico tutto pieno, e allora cambiamo la modalità di rappresentazione. Per ogni punto sull'asse verticale, da 0 a 1, teniamo conto di quante volte esso viene toccato: infatti i 100000 punti che hai calcolato non si distribuiscono uniformemente su quell'intervallo. Ad ogni punto associamo allora un livello di grigio proporzionale a quante volte esso è stato toccato. Ed ecco quello che salta fuori:».
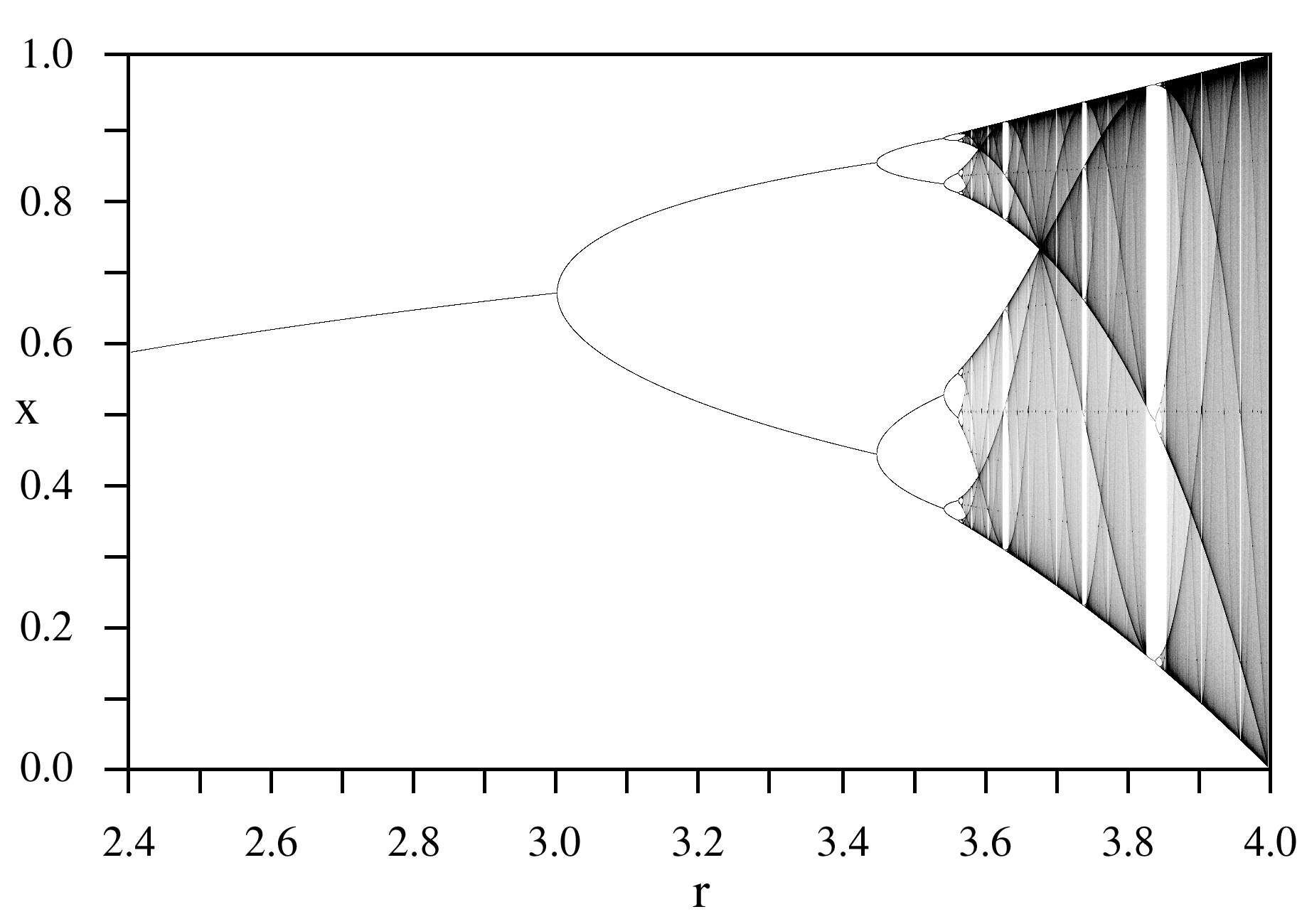 |
| Grazie a wikipedia per questa immagine. |







Nessun commento:
Posta un commento